[sorry, post tecnicistico il cui senso si spiega col prossimo]
Per definire ricchi e poveri ci possiamo avvalere del rapporto della banca d’Italia intitolato “La ricchezza delle famiglie italiane – anno 2011“, scaricabile qui che è anche stato ampiamente citato per l’affermazione controversa “Alla fine del 2011 la ricchezza netta … era pari a … poco più di 140 mila euro pro capite”.
Il rapporto dà i valori del coefficiente di Gini per i redditi (0,351), per la ricchezza netta (0,624), per le attività reali (0,628), per le attività finanziarie (0,779) e per le passività finanziarie (0,911). Tenendo conto che valori bassi di questo coefficiente indicano una distribuzione abbastanza omogenea, mentre valori alti indicano una distribuzione più diseguale, in Italia i ricchi per reddito sono pochi, ma ancora meno sono i ricchi per patrimonio. E tra i ricchi per patrimonio ancora meno sono quelli che detengono molte attività finanziarie.
Da questi fatti, due semplici deduzioni che non richiedono una laurea in economia:
- poiché una ricchezza patrimoniale è tale se genera dei redditi, dovrebbe esistere una proporzionalità tra ricchezza reddituale e ricchezza patrimoniale; siccome però la ricchezza concentrata tra le mani dei pochi non li rende altrettanto ricchi in termini di redditi, delle due l’una: o hanno in mano una ricchezza fasulla che non genera flussi (improbabile) oppure i flussi che genera sono occultati;
- se io fossi un potente lobbista, ex piduista, pseudo-centrista, e volessi fare gli interessi dei miei amici, preferirei le tasse sui redditi rispetto a quelle sui patrimoni, e tra quelle sui patrimoni quelle sulla ricchezza reale (= immobili) rispetto a quelle sulla ricchezza finanziaria.
Il rapporto della banca centrale non fornisce la Curva di Lorenz per queste distribuzioni, ma è possibile stimarla per la ricchezza netta sulla base dei valori di ricchezza detenuta dal 10 per cento delle famiglie più ricche (45,9%) e dal 50 per cento delle famiglie più povere (9,4%). Il grafico risulta così:
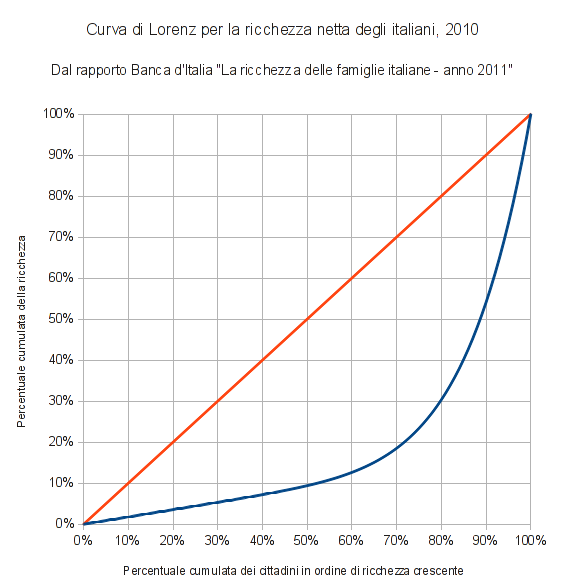
Per chi volesse verificare il reverse engineering, la curva è rappresentata dalla funzione: lorenz(x)=(E1*x+F1*x^G1)/(E1+F1) dove i parametri E1, F1 e G1 valgono 0, 4616881092; 2,1387053724 e 7.2982112159. La curva riproduce perfettamente il valore riportato per l’indice di concentrazione di Gini (0,624), il che fa pensare che sia la stessa forma funzionale usata dei tecnici della banca centrale. Tra l’altro il coefficiente di Gini di questa famiglia di curve di Lorenz è esprimibile analiticamente come: 1-(2*(E1*G1+2*F1+E1))/((F1+E1)*(2*G1+2)).
La disponibilità di questa curva ci permette di ricondurla alla forma del Principio di Pareto dicendo che il 25% dei ricchi possiede il 75% della ricchezza netta. Possiamo ottenere i valori 20/80 considerati universali da Vilfredo Pareto manipolando i coefficienti F1 (4) e G1 (9); a questa curva corrisponde un coefficiente di Gini di 0,717. Portandoli a 6 e 12 otteniamo Pareto 84/16 e Gini 0,786 che è vicino al valore indicato dalla banca centrale per la concentrazione delle attività finanziarie. Infine portandoli a 18 e 30 otteniamo Pareto 9/91 e Gini 0,912 che corrisponde alla concentrazione delle passività finanziarie.